Linear Discriminant Analysis Introduction

Introduction

Linear Discriminant Analysis (LDA) is a method to discriminate between two or more groups of samples. In order to develop a classifier based on LDA, you have to perform the following steps:
 

definition of groups

definition of discriminating function

estimation of discriminating function

test of discriminating function

application

Definition of groups:
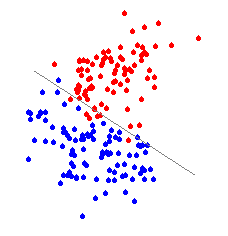
The groups to be discriminated can be defined either naturally by the problem under investigation, or by some preceding analysis, such as a cluster analysis. The number of groups is not restricted to two, although the discrimination between two groups is the most common approach. Note that the number of groups must not exceed the number of variables describing the data set. Another prerequisite is that the groups have the same covariance structure (i.e. they must be comparable).
 
Definition of discriminating function:
In principle, any mathematical function may be used as a discriminating function. In case of the LDA, a linear function of the form

y = a₀ + a₁x₁ + a₂x₂ + ..... + a_nx_n is used, with x_i being the variables describing the data set. The parameters a_ihave to be determined in such a way that the discrimination between the groups is best. Note that this linear discriminating function is formally equivalent to the multiple linear regression. In fact, one can directly use MLR if the response variable y is replaced by the weighted class numbers c₁ and c₂:

c₁ = n₂/(n₁+n₂)    and    c₂ = - n₁/(n₁+n₂) In order to get a better understanding of the working of  the discriminating function, start the following .
 

Estimation of the parameters of the discriminating function: As you have seen in the interactive example above, there is only one direction of the discriminating line which yields the best separation results. The determination of the coefficients of the discriminating function is quite simple. In principle, the discriminating function is formed in such a way that the separation (=distance) between the groups is maximized, and the distance within the groups is minimized.
 
Test of the discriminating function
When the discriminating function is parametrized, it has to be tested either by using an independent set of test data, or by performing cross-validation. In both cases, the results of the test set should be comparable to the training data.
 
Application
Discriminant analysis can be used to perform either analysis or classification:
 

• Analysis: How can the material be interpreted? Which variables contribute most to the difference?
• Classification: Given that a discriminating function can be found which provides satisfactory separation, this function can be used to classify unknown objects.

source: http://www.vias.org/tmdatanaleng/cc_lda_intro.html